How does std::sort work? Have you ever wondered about std:sort? Popping under the hood and understand what is actually going on when we want to perform a sorting operation?

It is always interesting to take a look and see what powers the STL, something we take for granted and always reach for.

Sorting

Sorting is not a difficult concept. We have a group of Foos that have a property which make them comparable to each other, positively stating that, as an example, Foo a < Foo b. This is usually easier said than done, sorting objects is a thoroughly research domain and there are numerous sorting algorithms, adequate to a plethora of different use cases. For every single one out there, there are even more variations that improve their performance, whether that means runtime performance, storage size, etc.

Not only that but in the last few years, specialized hardware targeting different and specific workloads, has been developed. This specialized hardware excels at specific workloads, operations on integers for example, and benefits from other improvements (i.e. vector operations), attempting to squeeze every bit of performance they can.

During University classes, maybe on Algorithms 101, there is usually some time dedicated to introduce students to well known sorting algorithms. QuickSort, HeapSort, InsertionSort, Bubble sort, which should be familiar names, are some of the most common sorting algorithms. Some have real world applications while other might be standing on the realm of academic do’s and dont’s.

It is not surprising that some of these come naturally to humans. As an example, when going through a phone book, if we are searching for John, intuitively, we might open the book in some location that we assume that is close to names starting with the letter J. If we go beyong it, we could take the left portion of the book, try to find its middle in an attempt to cut our search short. This is a simple example illustrating binary search.

These days, language standard libraries provide implementations that we, developers, make use of. That is exactly the case for C++ programmers, when reaching out for sorting algorithms that the different STL implementations provide.

As we go through the Sort entry under CppReference, we are greeted with plenty information on how sort works, what it does, and how efficient it is. With its complexity of O(N log N), we can take a guess that somehow, QuickSort or HeapSort are the machinery powering the STL implementation. That was true up until LWG713 came into the picture. Up until then, Sort used to be implemented using QuickSort, reflecting the complexity specified on cppreference. But, it makes no mention of the worst case of O(N2) that burdens this algorithm.

Before going any further, answering the question “Which sorting algorithm does the STL use?” gets a “it depends”.

LWG713 and O(N log N)

Such a small piece of text, provided a rather big change when it comes to STL implementations. This change states that the wording for sort is too lax and complexity should be O(N log N), even in the worst case scenario.

This meant that STL implementors needed to take action moving from something like QuickSort, and implement David Musser’s variant called “Introsort”.

Introsort is an hybrid algorithm that doubles down on the strengths of QuickSort, HeapSort, and even InsertionSort. The first two algorithms should not take anyone by surprise as the complexity is in line with LG713 recommendation of O(N log N). But why is InsertionSort making an appearence there? The answer lies in data locality and how a computer works, more specifically, how it is architectured. I repeat what others before me have said, memory access is expensive, so it is important to be considerate of it. This is one more of the numerous examples that show that. For the past few years, maybe decades, we have been freeloading on Hardware improvements allowing ourselves to relax and forget what is going underneath all the magic. I will not to go into too many details on the hardware/architecture level since that is not the main focus of this entry.

When the number of elements that needs sorting is small, it will be faster to bring them all into the same cacheline (or have them readily available on L1 Cache) and perfom the sorting operation on them, taking advantage of readily available elements on cache, and not being necessary to access main memory. With this, when small elements require sorting, we will incur in fewer cache misses and although the machine might have to execute a greater number of instructions, each one will execute faster, given that the data is readily available. We are taking advantage of what the CPU gives us. There is an interesting paper by LaMarca and Ladner titled “The Influence of Caches on the Performance of Sorting” which revolves around the gains for cache-conscious design. And that is the beauty of Introsort, it builds on the strenghts of each algorithm, using the one most approriate for each scenario where it shines.

Introsort attempts to find a fine balance between the platform that your software will run on and algorithmic efficiency. With added insights into your code, libcxx will try to find the optimal balance between hardware and software.

I am going to refer to libcxx throughout this entry. Even though I have not read both GCC or MSVC implementations for their libraries, let’s say that it matters not the actual implementation when all of them are following the same specification.

Throughout this entry, there are some simple benchmarks illustrating the points above.

Benchmarks

For this scenario I used different algorithms, some of them with different optimizations. We can clearly see the effects on the different sorting algorithms. The paper mentioned above goes into greater detail, refer to it if something is not clear. For the benchmarks, each algorithm ran with different different random integer numbers as inputs. I understand that the benchmark’s granularity could have been improved by feeding the algorithms a more diverse range of inputs. For the purpose of demonstrating the effects of caching in sorting algorithms, this will suffice. Algorithms used:

• BubbleSort
• BubbleSort Optimized
• InsertionSort
• InsertionSort Optimized
• HeapSort
• MergeSort
• QuickSort
• RadixSort
• std::sort

As expected, std::sort implementation in libcxx of the sorting algorithm uses introsort but also throws in some other ideas into the mix:

• option of using block quick sort for partitioning,
• guarded and unguarded InsertionSort for small lengths,
• Tuckey’s ninther technique for computing the pivot,
• check on whether partition was not required. The implementation is partly based on Orson Peters’ pattern-defeating QuickSort, published at: https://github.com/orlp/pdqsort. For the intrepid and curious, I defer you to Wikipedia’s page for Introsort when looking into its details.

Both the benchmarking binary and Google Benchmark were compiled with Clang and libcxx.

Before benchmarking any piece of code, I usually start with some assumptions, they always come as a reminder as to why we measure. Assumptions always have the same effect on me. They help me realize that despite them, the reality is somewhat different from how I perceive it. One does get better at making assumptions but they’re still that, guesses, when what we want are certainties.

Results

These results are only for visualisation purposes. Starting with a global view, the trends are clearly pictured. Nothing surprising.

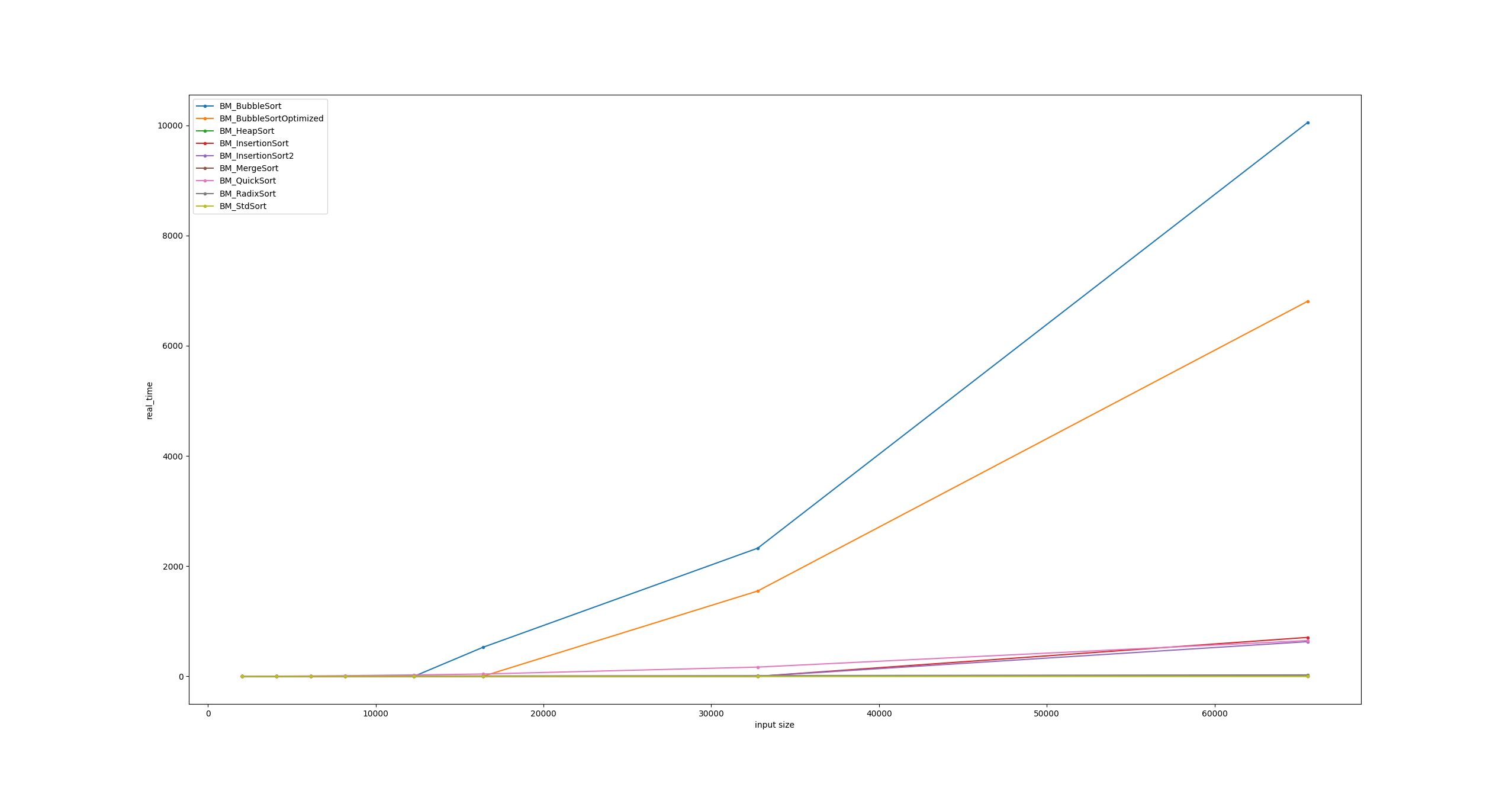
QuickSort and Radix have a better running complexity but that comes at the cost of a “slow start”. This becomes evident when zooming in on the beginning of the graph.

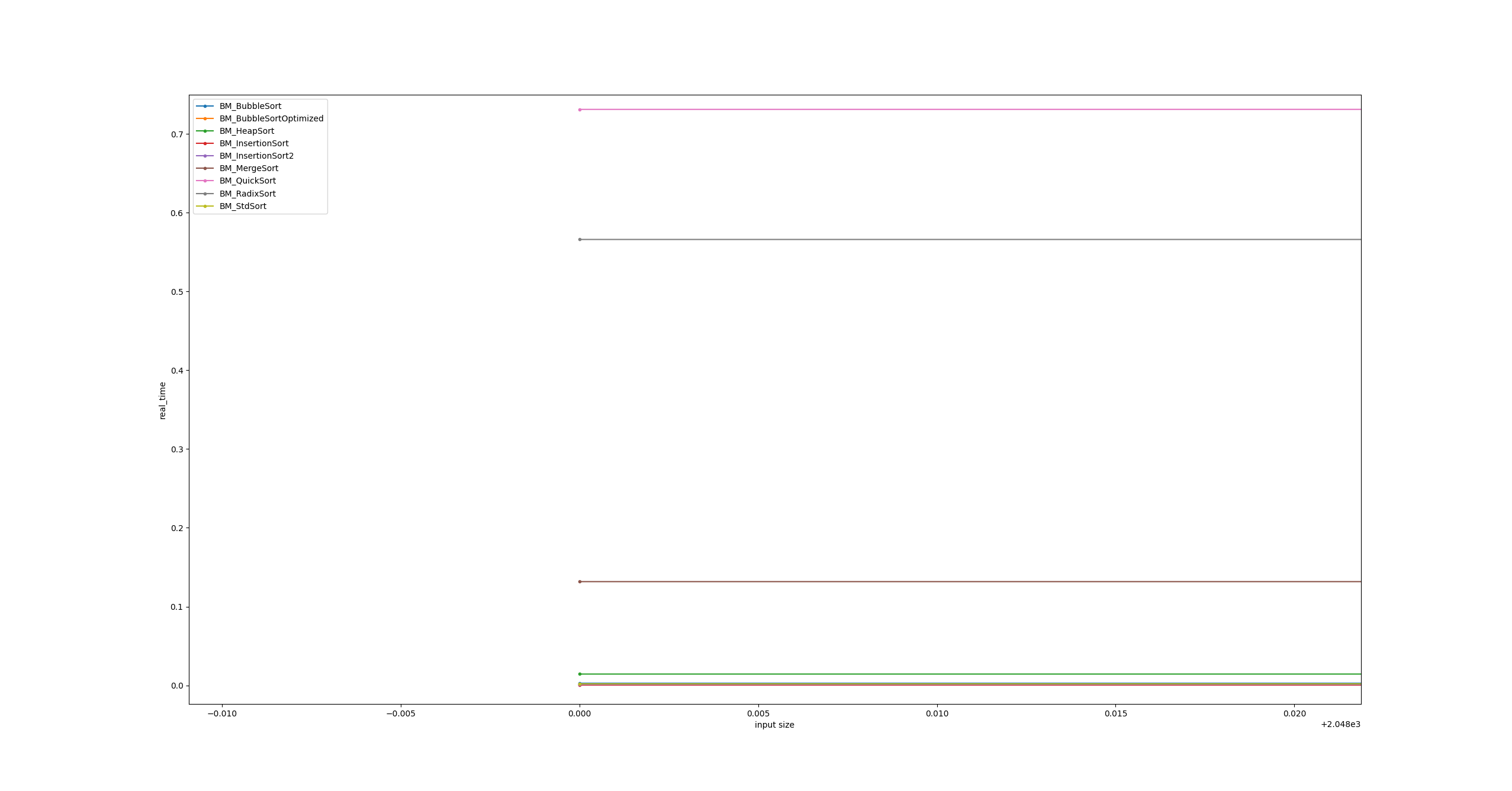
Going even further, it’s possible to see the worse complexity algorithms smoking the other on this very particular situation. This glory, as seen from the first image, is short lived on larger inputs.

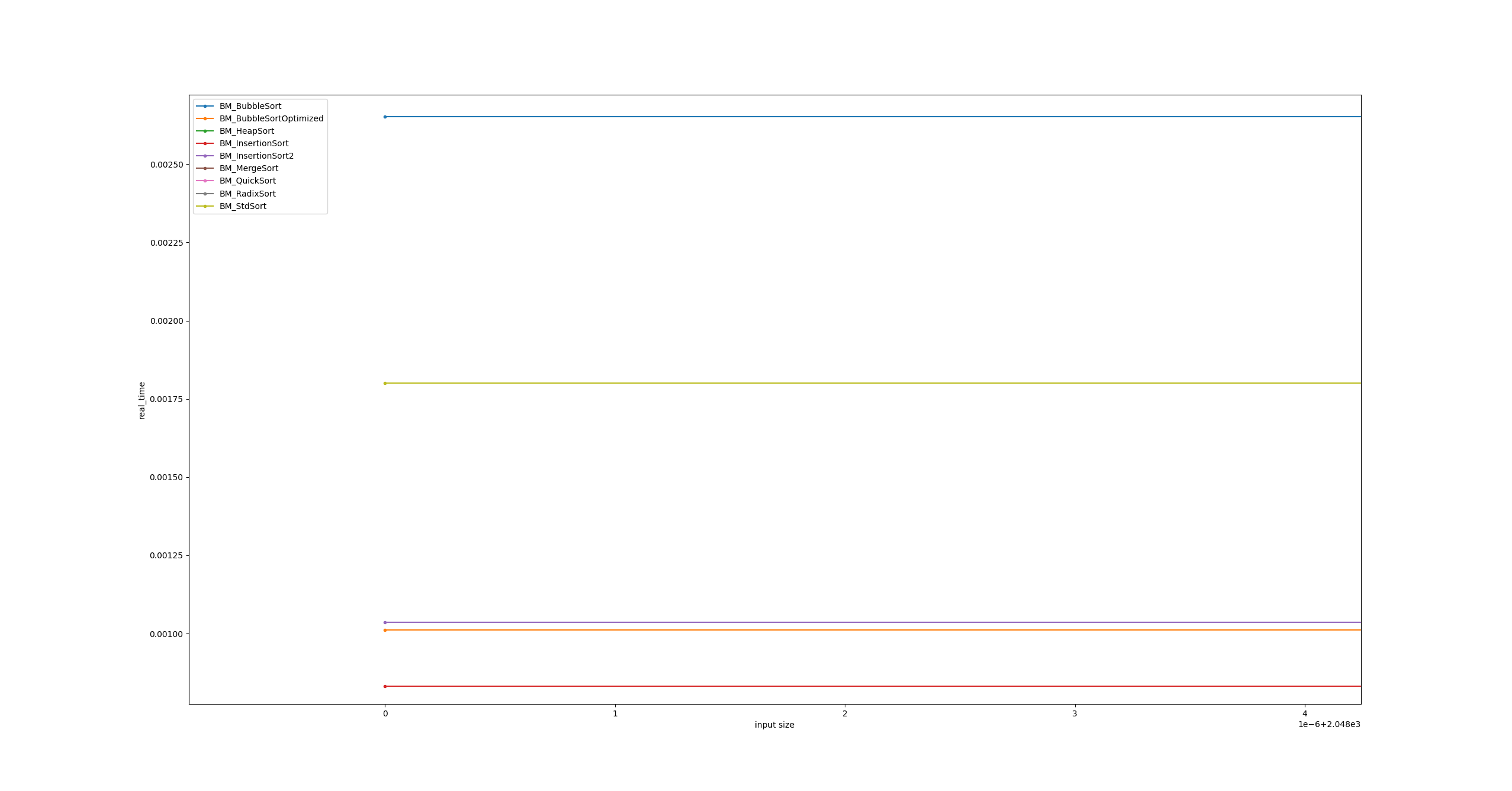
As soon as the workload starts increasing, the slower algorithms take the spotlight in not the most surprising ways.

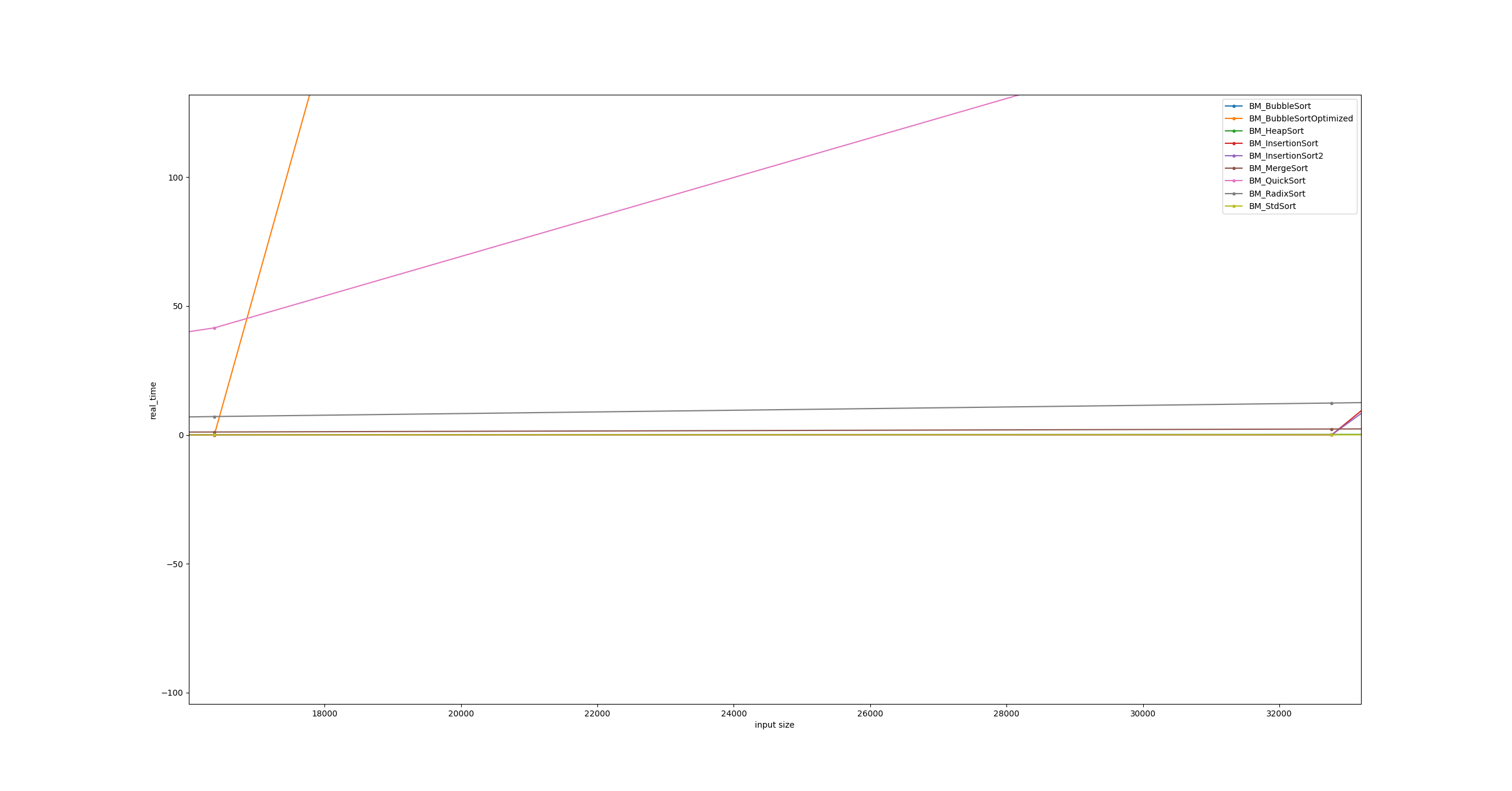
The observed jumps occur in the cache boundaries of the CPU that ran the tests. These should not come as a surprise since it is known that having data readily available on registers, L1, L2 or L3 Caches pays off.

On smaller inputs it does payoff to use a cache friendlier algorithm. Radix sort is the exact opposite in this case, but it does shine when used on bigger inputs because of its running complexity.

A good sorting implementation is aware of architectural details to take advantage of the hardware it is running on. Nonetheless, the STL also tries to be as flexible as possible, and this generalization also comes at a cost on different implementations.

When designing or working with loads that need sorting, we can rely on our tools to do the heavy lifting for us but that does not mean we are excused of understanding their inner workings.

I suspect if I had ran this on an MacBook I would also get different results since the cache line size for the M Series laptops is 128 bytes in size. Obviously, the different cache levels also make a dent on the running times but with this I want to turn your attention to the fact that knowing the small details of the target machine your workload is running will also make a big difference. That, and as we have seen, the input data. Results vary wildly and sometimes performance does matter.

I want to reiterate that these are not comprehensive analisis but rather illustrative examples, serving as a reminder that in the current year these details matter. Not only that and I am glossing over different details, for example, L3 Cache is usually shared by multiple cores while L1 and L2 are specific to one. Maintaining these Caches coherent requires being aware of how these specific Hardware details. This is a non-exhaustive list of different components that can negatively (or positively) affect runtime performance.

Conclusion

Not knowing about hybrid algorithms and being increasingly more aware of how important is to structure Software projects around the target, learning about Data Oriented Design, Performance and Optimizations in general, it was still surprising finding out about this implementation.

Curiosity led me into this side-quest and I got some detailed knowledge on how std::sort operates. I learned to appreciate these little challenges, when to take them and when not to get too side-tracked as to lose sight of my goals.

Knowing your domain, your target machine, and your usual load, helps architecting your solutions achieving their best. And this is exactly what businesses are doing, looking into their data to take the best decisions based on it.

Notes

As an aside, when I was going through libcxx’s code I found out that it also has an implementation of SelectionSort which is only used when looking for the nth_element.